A Priori
A Priori (“from the earlier”) knowledge is knowledge that is independent of experience. Knowledge by reasoning from definitions formed or principles assumed (eg, 'All bachelors are unmarried).  A Priori knowledge is also related to intuition.

Galen Strawson wrote that an a priori argument is one in which "you can see that it is true just lying on your couch. You don't have to get up off your couch and go outside and examine the way things are in the physical world. You don't have to do any science."

The counter to a priori knowledge is a posteriori knowledge (“from the later”) – knowledge dependent on experience or empirical evidence (eg, ‘Some bachelors are very happy’).  A posteriori justification makes reference to experience; but the issue concerns how one knows the proposition or claim in question —what justifies or grounds one's belief in it.

Plato posited in the Meno that we are able to have ‘a priori’ knowledge owing to a pre-natal close encounter that our disembodied souls had with the Forms. Descartes posited in the ‘Meditations on First Philosophy’ that such knowledge is infallible because guaranteed by a non-deceiving God.

When Thomas Jefferson stated in the Declaration of Independence - 'we hold these truths to be self-evident' - that's a form of a priori knowledge.  Jefferson was influenced by the Stoics’ view of truths. When such ideas are presented to us, they immediately become irresistible, naturally, spontaneously so. 

Human beings have special non-empirical cognitive capacities that yield what are called “rational intuitions”.  Authentic a priori knowledge permits rational intuitions to act as sufficient justifiers of beliefs about propositions or necessary truths. In regard to contemporary philosophy, intuition-skeptical empiricism has been deemed arguably false, however intuition-skeptical attacks on rationalism remain unanswered.

A Priori Zen

Analytic–Synthetic Distinction
The analytic–synthetic distinction is a semantic distinction – the meaning of words in regard to truth values or conditions of a sentence’s proposition.  The distinction was first proposed by Immanuel Kant. It was revised considerably over time with different philosophers have used the terms in very different ways.  Many of the formal approaches to semantics in mathematical logic and computer science originated in early 20th-century philosophy of language and philosophical logic.  Gottlob Frege and Bertrand Russell were highly influential of that period.
A review of the basic sentence structure is helpful before exploring the “Analytic-Synthetic” distinction.  A complete sentence has two parts: 1) Subject, 2) Predicate.

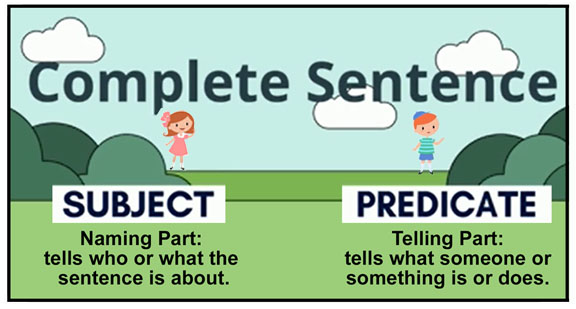
Analytic: the predicate is wholly contained in the subject. The proposition just ‘unpacks it’. Necessarily true. “Bachelors are unmarried males”. The concept ‘bachelor’ contains the concept ‘unmarried’; ‘unmarried is part of the definition of the concept ‘bachelor.  Likewise for the statement: “All triangles have 3 sides”.  Analytic statements can be proven true by analyzing their terms (they are tautological).

Synthetic: the predicate is wholly distinct from the subject but adds to the subject. A synthetic proposition is a proposition that is capable of being true or untrue based on facts about the world - in contrast to an analytic proposition which is true by definition. "All bachelors are unhappy" is a synthetic proposition since its truth depends upon experiencing all bachelors.

In the Critique of Pure Reason, Kant conjoins analytic-synthetic propositions with a priori and a posteriori proposition yielding four possible types of propositions:

1) analytic a priori – rational statements can only be analytic a priori statements meaning that propositions not based on experience can be shown to be true by their linguistic terms (ie, subject/predicate ‘coupling’). Empiricist (eg, Hume) support the analytic a priori distinction.
2) synthetic a posteriori – empirical statements can only be synthetic a posteriori statements meaning that the propositions based on experience cannot be showed to be true by their linguistic terms alone (ie, subject/predicate disconnect).  Empiricist support the synthetic a posteriori distinction.
3) synthetic a priori – The empiricists hold that there is no synthetic a priori truths whereas the rationalists hold that these types of truth exist.  In ‘Kant Crosses Hume’s Fork' Kant proved the existence of a synthetic a priori statements – not permitted by Hume.  Kant used mathematics, especially geometry, as a model for synthetic a priori judgments. They are necessarily and universally true (a priori); but their truthfulness is not dependent or based upon mere definitions (ie, they are also synthetic). Kant concluded that mathematical propositions were synthetic a priori statements. For example, 48+22 = 70 is synthetic because it requires references to concepts outside of itself for its truth. The concept "70" doesn't necessarily contain "48+22". Newton’s second law of motion states that the force on an object is proportional to the product of its mass and the acceleration. F=ma is necessarily true and not tautological, yet only indirect evidence can prove it (we can’t observe force, mass, and acceleration directly). Similarly with Einstein’s energy-mass equivalence equation.  E=mc2 is true but we cannot confirm it with direct experience.  Likewise, spacetime is a synthetic a priori concept that “is real” and “useful” and tells us facts about the world outside of us.
4) analytic a posteriori – Kant concluded that the analytic a posterior proposition was a contradiction since it could not be the case that the content of the predicate is already contained within the concept of the subject and that the proposition relied on observation to be true.

Rebuttal
Bertrand Russell, Gottlob Frege, and the logical positivists were not persuaded by Kant’s argument that mathematics was synthetic. For them, mathematical (and logical) statements were purely analytic. Frege used the idea of substituting synonymous terms. "All bachelors are unmarried" can be expanded out with the formal definition of bachelor as "unmarried man" to form "All unmarried men are unmarried", which is recognizable as tautologous.  Similarly, 7+5 = 12 is expanded to 12 = 12.  According to Frege's, et al, logical semantics arithmetic truths like "7+5=12" are no longer synthetic a priori but analytical a priori truths.