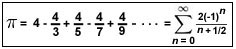Math Timeline

30,000 B.C. – Paleolithic peoples in Europe make number marks on bones.

2,000 B.C. – Babylonians use symbols for numbers; they observe that pi is approximately equal to 3.

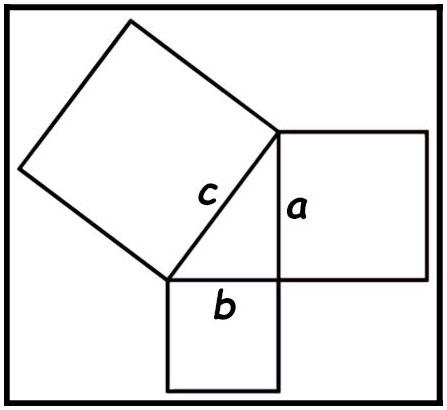
570 B.C. - Pythagorean theorem. 
The lengths of the three sides of a right triangle have the mathematical relation: c² = a² + b².   Visual Pythagorean.

c. 300 B.C. – Euclid’s Elements is compiled. 
Euclid proves there are infinitely many prime numbers.  He also mathematically describes the five Platonic solids (tetrahedron, octahedron, cube, icosahedron, dodecahedron) and argues that there are no further convex regular polyhedra.

1202 – Leonardo of Pisa publishes the Liber Abaci and introduces the sequence of Fibonacci numbers.
Each number in the Fibonacci sequence is the sum of the two preceding numbers starting with the root number one:  1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc.  The ratio of two adjacent Fibonacci numbers progresses towards the Golden Mean (144/89 = 1.618).  The Fibonacci sequence and Golden Mean ratios appear everywhere in the universe.  The spiral is the natural pattern of water flowing drown a drain; the flow of air in tornados and hurricanes; the spiral form of the Nautilus shell; the number of lines in the spirals of a sunflower; the spiral of a galaxy.  The Golden Mean ratio is also all over the human body: the ratios between bones and the length of your arms and legs; the ratio in the distance from the navel to your toe and the distance from your navel to the top of your head.

~1380s - The formula for pi first discovered by Madhava of Sangamaram.
Not widely known in the west.  Leibniz was the first person to rediscover the series in continental Europe (sometimes called Madhava-Leibniz series).

1560s – Christiaan Huygens and Blasie Pascal discuss the foundations of a theory of probability.

1637 – Rene Descartes invents the Cartesian coordinate system.
Revolutionizes mathematics by providing the first systematic link between Euclidean geometry and algebra.

1666s-1670s – Isaac Newton and Gottfried Leibniz take first steps in the Differential and Integral Calculus.

1773 – Abraham de Moivre publishes work on the normal distribution as an approximation to the binomial distribution of probabilities.

1735 – Leonhard Euler solves the Konigsberg bridge problem and prepares the way for a theory of graphs.

1780 – Leonhard Euler explores the notion of a Latin square, the forerunner of modern Sudoku.

1801 – Carl Friedrich Gauss publishes Disquitiones Arithmeticae and includes the construction of the regular 17-sided polygon by ruler and compass.

1829-1831 – Nikolai Ivanovich Lobachevsky and Janos Bolyai independently publish work on “non-Euclidean” hyperbolic geometry.

1832 – Evariste Galois proposes the  idea of groups of permutations in connectin with the theory of equations.

1847 – George Boole publishes the Mathematical Analysis of Logic and paves the way for the language of the modern programmable computer.

1858 – Arthur Cayley publishes his definitive paper on the “Theory of Matrices,” a theory in algebra with far-reaching consequences.

1859 – Bernard Riemann puts forward the famous “Riemann hypothesis” as a conjecture. 
Riemann discovers that the zeros of the zeta function (complex infinite series) occur in a regular pattern precisely on a line that extends to infinity.  He proposes that the distribution describes the pattern of prime numbers. In 1973, Hugh Montgomery learns that the occurrence of Riemann’s zeros matches the pattern of energy levels of excited nuclei (pair correlation conjecture).  As of 2004, 10²⁴ zeros have been determined by using computers.  Although the Riemann hypothesis remains formally unproven, most mathematicians now accept it as true.

1874 – Georg Cantor introduces a controversial notion of infinity.  

Proves that there are different types and sized of infinities (the infinite set of whole numbers is smaller than the infinite set of decimals). 

1880s – Francis Galton, a cousin of Charles Darwin, introduces ideas on regression and correlation in statistics.

1882 – Ferdinand von Lindemann proves that pi is a transcendental number and consequently “squaring the circle” is impossible.

1889 – Henri Poincare encounters chaos in his entry for a competition in honor of Sweden’s King Oscar II.

1890 – Giuseppe Peano constructs his famous space filling curve prompting an overhaul of the theory of curves.

1900 – David Hilbert suggests 23 famous problems as an agenda for mathematicians of the 20th century.
Four problems remain formally unproven, the 8th being the most notorious (Riemann hypothesis). In his early work, Hilbert showed that a finite set of equations spawn an infinite number of equations, although he was unable to construct the originating set of equations.  Critics claim that, in proving that something must exist without actually producing it, Hilbert strayed from mathematics into theology.

1930 – Bartel van der Waerden publishes his famous Moderne Algebra, which sets out the method of the new algebra.

1931 – Kurt Godel proves that it is possible for a formal mathematical system to contain undecidable statements.

1946 – ENIAC the first general-purpose electronic computer comes into operation.

1947 – George Dantzig outlines a theory of linear programming and formulates the Simplex algorithm.

1975 – Benoit Mandelbrot introduces fractals into geometry and indicates their widespread application.

1983 – The classification of finite simple groups is achieved and the so-called “Enormous theorem” is finally accomplished.

1994 – John F. Nash is awarded the Nobel Prize for Economics for his work on game theory.

1994 – Andrew Wiles proves “Fermat’s last theorem” and collect the Wolfskehl prize.
Fermat's Last Theorem states that no three positive integers a, b, and c satisfy the equation aⁿ + bⁿ = cⁿ for any integer value of n greater than 2.

2001 – Grigori Perelamn completes the proof of the Poincare Conjecture by establishing the result for dimension 3.